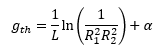
For any laser to function, there must be more gain inside the laser cavity than loss, and the point at which the laser gain is just large enough to overcome the cavity loss enabling lasing is called gain threshold. While simple, in theory, this concept of gain threshold can be particularly challenging to understand, particularly when it comes to diode lasers. Therefore, as part of our ongoing blog series expanding on the topics covered in our Lasers 101 section, we are going to explore the concept of laser diode gain threshold in this blog post. This will require us to take a look at not only the causes of cavity loss in a laser diode but also the fundamental mechanisms behind optical amplification and gain in the diode material itself.
Direct bandgap semiconductor materials can be used as both optical emitters (lasers and LEDs) and optical absorbers (photodetectors), so how does one make the same material structure operate in these two diametrically opposite states? The answer lies in whether or not the diode is in a state of population inversion. Population inversion occurs when there are more electrons in the conduction band than in the valence band, and when this happens, the material is capable of producing stimulated emission or what is commonly referred to as gain. When the diode is not experiencing population inversion, and there are more electrons in the valence band than the conduction band, making the diode an absorber instead. Therefore, the first thing we need to understand is how population inversion is achieved inside a diode to produce gain. Once we have reviewed this topic, we can then take a look at the losses in a laser diode, to develop a full understanding of gain threshold.
In material science, the energy level at which there is an equal probability of having either an electron or a hole is called the Fermi energy. Therefore, at an energy level less than the Fermi energy, there is a higher probability of an electron, and at energy levels greater than the Fermi energy, there is a higher probability of a hole. For population inversion to take place then the Fermi energy must be greater than the conduction band energy, unfortunately, in semiconductors, the Fermi level falls in the exact middle of the bandgap between the valence and conduction bands. This means that under normal conditions the semiconductor will never achieve population inversion because there can never be more electrons in the conduction band than holes. However, if a significantly large current is injected across the PN-junction of the diode, it can induce a quasi-equilibrium state causing the Fermi level to split into two quasi-Fermi levels decoupling the electron and hole density probabilities from each other. Once these quasi-Fermi levels are induced, the electron density in the conduction band becomes a function of current and to a lesser degree temperature. Therefore, making the population inversion directly proportional to the drive current.
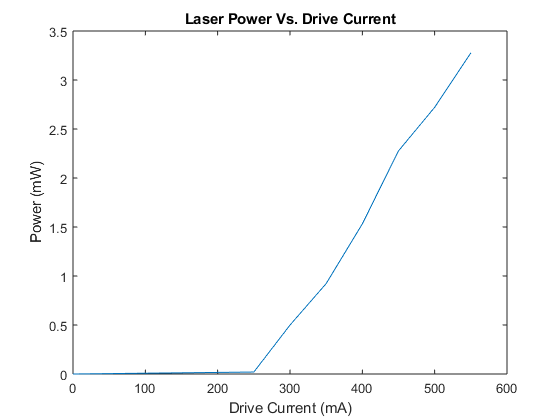
In the image below, you can see the L-I curve for an 830nm multi-mode laser diode, showing the relationship between output power and drive current. From this plot, it can be seen that after a minimum current threshold is reached the laser’s output power increases linearly with drive current. As the current is increased the, Fermi level splits achieving population inversion, creating gain, and then once the gain reached a certain threshold began to lase. This is a clear example of the presence of gain threshold.
Now that we have a clear understanding of the cause of gain in laser diodes, we can take a look at the losses in the system that inevitably determine where that threshold lies. The primary source of loss in any laser comes from the reflectivity of the mirrors in the resonator cavity. While a full derivation of this relationship is beyond the scope of this blog post, it can be shown that the loss due to each mirror in the resonator is proportional to the natural log of the inverse of the reflectivity. While this may sound complicated, it merely means that the more reflective the mirrors are, the lower the total loss and therefore, the lower the gain threshold.
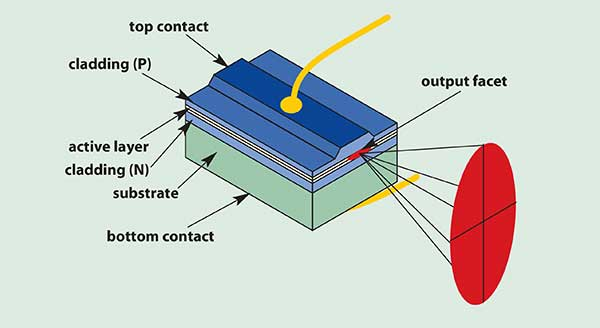
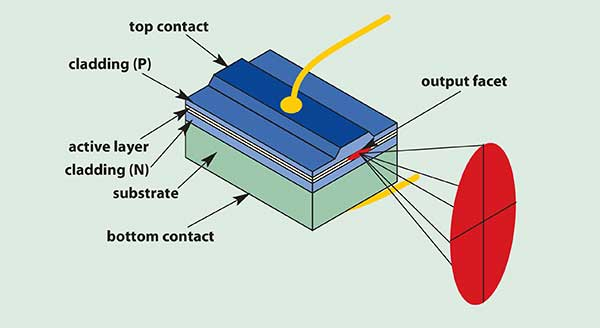
As we discussed in a previous blog post, semiconductor materials are unique among laser gain materials for their extremely high index of refraction, which results in each facet of the laser diode naturally acting as a partially reflective mirror (~32%). Therefore, a laser diode has a built-in resonator which is capable of lasing without any external optics or coatings. For higher power applications the rear facet of the laser diode is typically coated with a dielectric material to increase the reflectivity to over 90%. This HR mirror dramatically reduces the gain threshold while simultaneously increasing the useful power out of the front facet (or output coupler).
While there are other contributing factors just as scattering losses, absorption losses, and other defects in the diode structure; these all play a much smaller role in the overall system losses when compared to the mirror loss and therefore can be ignored in most cases. The last factor that must be looked at to understand the gain threshold is one that seems simple, but that is often overlooked, the size of the gain medium itself.
Simply put, the larger the gain medium, the more electrons present to generate photons. This is the reason why high power laser diodes are typically a much larger size than lower power laser diodes. When you combine the size of the diode with the losses discussed in the previous paragraph we can come up with the equation below, where gth is the gain threshold, R is the reflectivity of each facet, and a represents the other losses in the diode.
By understanding the relationships between the gain mechanisms of the semiconductor material structure and loss mechanisms associated with the laser diode’s built-in resonator cavity, it allows you to develop a fully formed understanding of laser diode gain threshold.
Here at RPMC Lasers, we have over 20 years of experience with diode lasers and are readily available to assist you in not only deciding which of our standard off the self-laser diodes are ideal for your application, but we are also able to offer countless custom laser diode packaging configurations with a wide range of integrated optics including all of the designs discussed above. For more information about our wide variety of laser diodes, you can click here, and for more information about laser diode fundamentals, be sure to visit our Lasers 101 page.

 SHIPS TODAY
SHIPS TODAY