Diode lasers are unique amongst most other laser sources for their extensive range of available wavelengths. The breadth of output wavelengths has allowed diodes to become one of the most versatile laser sources, with wavelengths available from ultraviolet to the infrared. To understand why semiconductor diodes have such a wide range of wavelength options, we must first take a look at the underlying physical principles behind energy levels and stimulated emission. After you have a working knowledge of three basic principles and how they determine the laser’s emission wavelength, we can then explore how these general concepts can be applied to the bandgap energy of a semiconductor and explain how laser diodes with nearly any wavelength are produced.
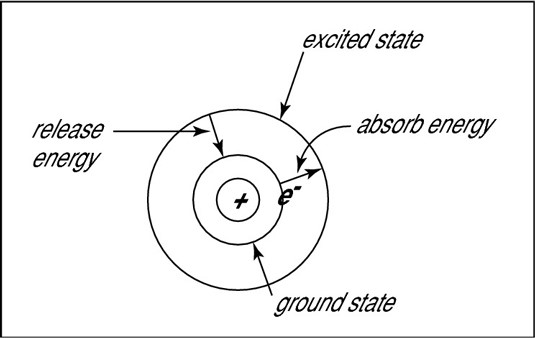
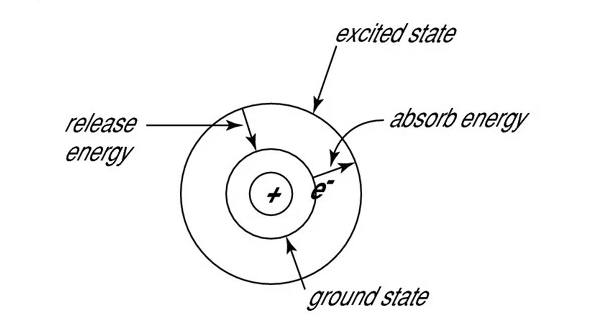
The word laser is an acronym for Light Amplification by Stimulated Emission of Radiation. For stimulated emission to take place, an atom or molecule must already be in an excited state. To be in an excited state, means the outer shell electrons (also known as the valence electrons) are somehow given enough energy to jump up to the next quantum energy level. A detailed explanation of the underlying quantum physics behind this process is beyond the scope of this blog post, but it is helpful to think in terms of the Bohr diagram shown below. In this analogy, the valence electron jumps from the stable ground state to a higher energy level after absorbing energy from an outside source. Since this excited state is not stable, the electron will quickly fall back down to the ground level and then release that energy in the form of a photon or a phonon. When a photon is emitted during this process, it is known as spontaneous emission, which is the fundamental process behind most traditional light sources ranging from fire to light bulbs. Furthermore, since the wavelength of the photon is inversely proportional to the photon’s energy, the size of the gap between these two energy levels will determine the wavelength of the emitted light. The relationship between wavelength and energy is why when an object heats up, it will initially start glowing red, and then the color will eventually begin to shift towards the blue end of the spectrum as the temperature increases.
If a photon whose wavelength is precisely equal in energy to the difference between two energy levels interacts with an atom or molecule before it relaxes back down to the ground state; it will instantly knock the electron back down to the lower energy level causing it to emit a second identical photon. Therefore, all of the emitted photons will be at precisely the same wavelength, with the same phase, and direction. This is the definition of stimulated emission, and is the underlying physical phenomena, behind the lasing process. For stimulated emission to be possible, there must be more atoms or molecules in this excited state than in the ground state, a condition known as population inversion. Population inversion can occur if the atom or molecule used as a gain medium has a metastable (or “kind-of-stable”) excited state which would allow for the electrons to build up. This means that the excitation wavelength of the laser will be solely determined by the difference between the medium’s metastable energy level and its lower lasing level.
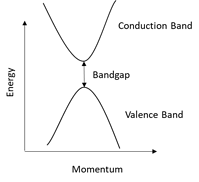
For monoatomic lasers such as gas lasers and most solid-state lasers, these energy levels are very well defined. But, since semiconductors have a much more complex molecular structure, the conduction and valence bands are far more “blurred” making it possible for the laser to be tuned over several nanometers. The diagram below shows an example of how, unlike in a monoatomic laser, semiconductor lasers have far more complex band structures.
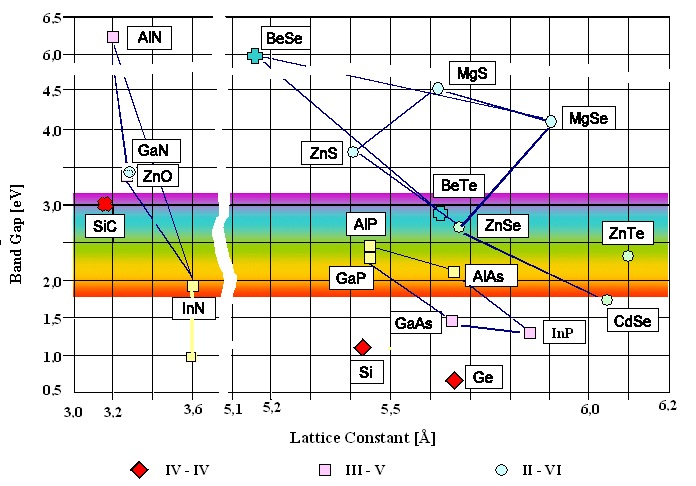
In addition to this, semiconductor devices can be engineered to have specific bandgap energy by combining various elements to form binary, ternary, and quaternary alloys. These semiconductors can have their bandgap further tailored by varying the stoichiometry in ternary and quaternary semiconductors. For example, blue and ultraviolet laser diodes can be designed by using a combination of AlN, GaN, and InN; and red and near-infrared laser diodes are made from blends of AlAs and GaAs. As a result, almost any bandgap energy can be engineered as long as you can match the lattice to the base semiconductor materials. The chart below does an excellent job of demonstrating the wide variety of semiconductors which can be matched to produce different bandgap energies.
While this was far from a comprehensive review of how the bandgap energy of a laser diode is determined, it hopefully has served as the foundation for you to understand its importance and how it allows diode lasers to be manufactured with such a wide range of different output wavelengths. Here at RPMC Lasers, we have over 20 years of experience with diode lasers and are readily available to assist you in not only deciding which of our standard off-the-shelf laser diodes are ideal for your application, but we are also able to offer countless custom laser diode packaging configurations with a wide range of integrated optics including all of the designs discussed above. For more information about our wide variety of laser diodes, you can click here, and for more information about laser diode fundamentals, be sure to visit our Lasers 101 page.

 SHIPS TODAY
SHIPS TODAY